Tutorial: Creating a Planning and Learning Algorithm

Tutorials (v1) > Creating a Planning and Learning Algorithm > Part 3

Q-Learning Overview

For our learning algorithm example, we'll be implementing Q-learning. The difference between a learning algorithm and a planning algorithm is that a planning algorithm has access to a model of the world, or at least a simulator, whereas a learning algorithm involves determining behavior when the agent does not know how the world works and must learn how to behave from direct experience with the world. In general, there are two approaches to reinforcement learning: (1) to learn a model of the world from experience and then use planning with that learned model to dictate behavior (model-based) and (2) to learn a policy or value function directly from experience (model-free). Q-learning belongs to the latter.

As the name suggests, Q-learning learns estimates of the optimal Q-values of an MDP, which means that behavior can be dictated by taking actions greedily with respect to the learned Q-values. Q-learning can be summarized in the following pseudocode.

Q-Learning

1. Initialize Q-values (Q(s,a)) arbitrarily for all state-action pairs.
2. For life or until learning is stopped...
3.     Choose an action (a) in the current world state (s) based on current Q-value estimates (Q(s,•)).
4.     Take the action (a) and observe the the outcome state (s') and reward (r).
5.     Update Q-value estimate for previous state-action pair (Q(s,a)) based on observed next state (s') and reward (r).

The two key steps in the above pseudocode are steps 3 and 5. There are many ways to choose actions based on the current Q-value estimates (step 3), but one of the most common is to use an ε-greedy policy. In this policy, the action is selected greedily with respect to the Q-value estimates a fraction (1-ε) of the time (where ε is a fraction between 0 and 1), and randomly selected among all actions a fraction ε of the time. In general, you want a policy that has some randomness to it so that it promotes exploration of the state space.

For updating the Q-value of the last state-action pair (s,a) with respect to the observed outcome state (s') and reward (r), Q-learning uses the following update rule:

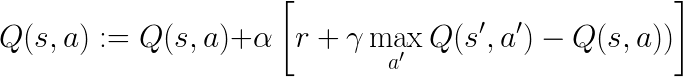
where α is a learning rate parameter between 0 and 1.

Recall from the Bellman equation that the Value of a state is the maximum Q-value and the Q-value is the expected sum of the reward and discounted value of the next state, where the expectation is with respect to the probability of each state transition. In the Q-learning update rule, the reward plus the max Q-value in the observed next state is effectively what the Bellman equation tells us the Q-value is, except in this case, we're not marginalizing over all possible outcome states, we only have the one observed state and reward that we happened to get. However, because our learning rate only allows our Q-value to change slightly from its old estimate to a new estimate in the direction of the observed state and reward, as long as we keep retrying that action in the same state, we'll see the other possible states that could have occurred and move in their direction too. In aggregate over multiple tries of the action then, the Q-value will move toward the true expected value, even though we never directly used the transition probabilities. To have guaranteed convergence to the true Q-value, we should actually be slowly decreasing the learning rate parameter over time. However, in practice, it's often sufficient to simply use a small learning rate parameter, so for simplicity in our implementation, we'll use a fixed value for the learning rate rather that one that changes with time (though in the full Q-learning algorithm provided in BURLAP, you can use different schedules for decreasing the learning rate, including client-provided custom schedules with the LearningRate interface).

Q-Learning Code

Lets begin implementing our Q-learning algorithm code. Our class, called QLTutorial, will extend OOMDPPlaner and implement the QComputablePlanner and LearningAgent interfaces. It might seem strange that we will extend the OOMDPPlanner class, since this is a learning algorithm; however, we sub class OOMDPPlanner because the class provides us a number of the same data members and methods we'll need. Moreover, Although not all planning algorithms could be used for learning, all learning algorithms can be used for planning, since learning problems could always be applied in simulation. Since Q-learning estimates Q-values, the QComputablePlanner interface lets that knowledge be conveyed to other BURLAP tools (like Q-derived policies). Finally, the LearningAgent interface specifies the common methods a learning algorithm is expected to implement so that it can be used by other BURLAP tools.

Below is the skeleton code that is created when we created our class, with the exception that we added an UnsupportedOperation exception to the planFromStateMethod. As noted above, we could implement planning by just simulating multiple learning episodes from the input state, but for this tutorial we will not bother.

import java.util.List;

import burlap.behavior.singleagent.EpisodeAnalysis;
import burlap.behavior.singleagent.QValue;
import burlap.behavior.singleagent.learning.LearningAgent;
import burlap.behavior.singleagent.planning.OOMDPPlanner;
import burlap.behavior.singleagent.planning.QComputablePlanner;
import burlap.oomdp.core.AbstractGroundedAction;
import burlap.oomdp.core.State;

public class QLTutorial extends OOMDPPlanner implements QComputablePlanner,
		LearningAgent {

	@Override
	public EpisodeAnalysis runLearningEpisodeFrom(State initialState) {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public EpisodeAnalysis runLearningEpisodeFrom(State initialState,
			int maxSteps) {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public EpisodeAnalysis getLastLearningEpisode() {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public void setNumEpisodesToStore(int numEps) {
		// TODO Auto-generated method stub

	}

	@Override
	public List<EpisodeAnalysis> getAllStoredLearningEpisodes() {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public List<QValue> getQs(State s) {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public QValue getQ(State s, AbstractGroundedAction a) {
		// TODO Auto-generated method stub
		return null;
	}

	@Override
	public void planFromState(State initialState) {
		throw new UnsupportedOperationException("We are not supporting planning for this tutorial.");
	}

	@Override
	public void resetPlannerResults() {
		// TODO Auto-generated method stub

	}

}
				

Similar to ValueIteration, the primary data we will want to store is a set of estimated Q-values for each state. We'll also again let the user specify the Q-value function initialization with a ValueFunctionInitialization object. We'll also need a learning rate parameter to be set. Finally, we'll need a learning policy to follow; that is, a policy that dictates how the agent chooses actions at each step. For this tutorial, we'll assume an ε-greedy policy and let the client specify the value for ε. Lets add data members for those elements now.

import java.util.Map;
import burlap.behavior.singleagent.ValueFunctionInitialization;
import burlap.behavior.statehashing.StateHashTuple;
import burlap.behavior.singleagent.Policy;
				

protected Map<StateHashTuple, List<QValue>> qValues;
protected ValueFunctionInitialization qinit;
protected double learningRate;
protected Policy learningPolicy;
				

Lets also add a constructor for all our data members.

import java.util.HashMap;
import burlap.oomdp.core.Domain;
import burlap.oomdp.core.TerminalFunction;
import burlap.oomdp.singleagent.RewardFunction;
import burlap.behavior.statehashing.StateHashFactory;
				

public QLTutorial(Domain domain, RewardFunction rf, TerminalFunction tf, double gamma, 
	StateHashFactory hashingFactory, ValueFunctionInitialization qinit, double learningRate, 
	double epsilon){

	this.plannerInit(domain, rf, tf, gamma, hashingFactory);
	this.qinit = qinit;
	this.learningRate = learningRate;
	this.qValues = new HashMap<StateHashTuple, List<QValue>>();
	this.learningPolicy = new EpsilonGreedy(this, epsilon);

}
				

Note that the EpsilonGreedy policy object we create takes as input the planning/learning algorithm that implements the QComputablePlanner interface, and the value for epsilon to use.

One of the primary tools we'll need is a method that grabs our Q-values, or creates and stores them with the proper initialization value if it's for an unseen state. Lets implement our Q-Value methods now.

import java.util.ArrayList;
import burlap.oomdp.singleagent.GroundedAction;
				

@Override
public List<QValue> getQs(State s) {
	
	//first get hashed state
	StateHashTuple sh = this.hashingFactory.hashState(s);
	
	//check if we already have stored values
	List<QValue> qs = this.qValues.get(sh);
	
	//create and add initialized Q-values if we don't have them stored for this state
	if(qs == null){
		List<GroundedAction> actions = this.getAllGroundedActions(s);
		qs = new ArrayList<QValue>(actions.size());
		//create a Q-value for each action
		for(GroundedAction ga : actions){
			//add q with initialized value
			qs.add(new QValue(s, ga, this.qinit.qValue(s, ga)));
		}
		//store this for later
		this.qValues.put(sh, qs);
	}
	
	return qs;
}

@Override
public QValue getQ(State s, AbstractGroundedAction a) {
	
	//first get all Q-values
	List<QValue> qs = this.getQs(s);
	
	//translate action parameters to source state for Q-values if needed
	a = a.translateParameters(s, qs.get(0).s);
	
	//iterate through stored Q-values to find a match for the input action
	for(QValue q : qs){
		if(q.a.equals(a)){
			return q;
		}
	}
	
	throw new RuntimeException("Could not find matching Q-value.");
}
				

The only part of that code that probably needs any additional elaboration is the translate action parameters part. Recall that in an OO-MDP (unless otherwise specified), two states can be identical even if the object names/references are different as long as there is a bijection between the objects of the states. (refer back to the Building a Domain tutorial for more information). Therefore, it's possible that the input state for which we're trying to get the Q-values is equal to a stored state that has different object identifiers. If our actions are not parameterized, there is no issue here. However, if actions are parameterized to objects in the world, we may need to map the parameters from the input state/action to the stored/state action before we can determine which corresponding action is a match. For example, if we were learning in a blocks world and the action was pickup block0 in our input state, but block0 corresponded to block6 in our stored stated, then we'd want to return the Q-value for pickup block6. The translateParameters method of our action takes as input a source state and a target state; then it finds a mapping for the parameters of the action in the source state to the target state and returns a new GroundedAction using those parameters. That is, if applied to "pickup block0", it would return "pickup block6".

For code clarity, lets also implement a method that takes a state and returns the maximum Q-value for the state.

protected double maxQ(State s){
	if(this.tf.isTerminal(s)){
		return 0.;
	}
	List<QValue> qs = this.getQs(s);
	double max = Double.NEGATIVE_INFINITY;
	for(QValue q : qs){
		max = Math.max(q.q, max);
	}
	return max;
}
				

One important element in that method to pay attention to is the fact that we first check if the input state is a terminal state and return 0 if it is. Like with our previous VI code, this check is important, because the definition of a terminal state is a state from which all action stops and we need to make sure they return max Q-values of of 0 when we update the Q-values for state action-pairs that lead to them.

Now that we have all of our helper methods, lets implement the learning algorithm. The LearningAgent interface requires us to implement two methods that cause learning to be run for one episode; one that will run learning until the agent reaches a terminal state and one that will run learning for a maximum number of steps or until a terminal state is reached. We well have the former call the latter with a -1 for the maximum number of steps to indicate that it should never stop until the agent reaches a terminal state. Both methods also require returning an EpisodeAnalysis object, which is a recording of all the states, actions, and rewards that occurred in an episode, so as we write the code to have the agent iteratively select actions, we'll record the results to an EpisodeAnalysis object.

Below is the learning algorithm code for Q-learning.

@Override
public EpisodeAnalysis runLearningEpisodeFrom(State initialState) {
	return this.runLearningEpisodeFrom(initialState, -1);
}

@Override
public EpisodeAnalysis runLearningEpisodeFrom(State initialState,
		int maxSteps) {
	
	//initialize our episode analysis object with the given initial state
	EpisodeAnalysis ea = new EpisodeAnalysis(initialState);
	
	//behave until a terminal state or max steps is reached
	State curState = initialState;
	int steps = 0;
	while(!this.tf.isTerminal(curState) && (steps < maxSteps || maxSteps == -1)){
		
		//select an action
		AbstractGroundedAction a = this.learningPolicy.getAction(curState);
		
		//take the action and observe outcome
		State nextState = a.executeIn(curState);
		double r = this.rf.reward(curState, (GroundedAction)a, nextState);
		
		//record result
		ea.recordTransitionTo((GroundedAction)a, nextState, r);
		
		//update the old Q-value
		QValue oldQ = this.getQ(curState, a);
		oldQ.q = oldQ.q + this.learningRate * (r + (this.gamma * this.maxQ(nextState) - oldQ.q));
		
		
		//move on to next state
		curState = nextState;
		steps++;
		
	}
	
	return ea;
}
				

You should notice that the code reflects our earlier written pseudocode for Q-learning quite closely! One thing you might be wondering is whether any action parameter translation might have needed to occur in the action selection, similar to how it needed to happen when matching Q-values up with a given action. It would; however, we actually do not have to worry, because our Q-value derived Policy classes (e.g., EpsilonGreedy) handle any necessary parameter translation from the Q-values to the input state automatically for us!

With that out of the way, we're just about finished. The last things we want to do are largely auxiliary. In particular, LearningAgent classes are asked to store the last N learning episodes so that they can be retrieved later. Lets add a data member for storing a list of the last set of learning episodes, how many to store, and then add to the end of our runLearningEpisode method code that adds the last episode to the list of most recent episodes (and removes old episodes if our storage is over the requested limit).

import java.util.LinkedList;
				

protected LinkedList<EpisodeAnalysis> storedEpisodes = new LinkedList<EpisodeAnalysis>();
protected int maxStoredEpisodes = 1;
				

while(this.storedEpisodes.size() >= this.maxStoredEpisodes){
	this.storedEpisodes.poll();
}
this.storedEpisodes.offer(ea);
				

Now we can implement the methods related to getting previous learning episodes.

@Override
public EpisodeAnalysis getLastLearningEpisode() {
	return this.storedEpisodes.getLast();
}

@Override
public void setNumEpisodesToStore(int numEps) {
	this.maxStoredEpisodes = numEps;
	while(this.storedEpisodes.size() > this.maxStoredEpisodes){
		this.storedEpisodes.poll();
	}
}

@Override
public List<EpisodeAnalysis> getAllStoredLearningEpisodes() {
	return this.storedEpisodes;
}
				

Finally, we can implement the resetPlannerResults method, which only needs to clear our Q-values.

@Override
public void resetPlannerResults() {
	this.qValues.clear();
}
				

Testing Q-Learning

As before, you can now test your learning algorithm with the previous code developed in the Basic Planning and Learning tutorial. Alternatively, you can use the below main method which creates the same Grid World domain and task as the test code we wrote for our VI implementation. Also as before, after learning for a number of episodes, it will take the greedy policy, roll it out once, and print out the actions taken. You should again find that only north and east actions are taken.

import burlap.behavior.singleagent.EpisodeAnalysis;
import burlap.behavior.singleagent.Policy;
import burlap.behavior.singleagent.planning.commonpolicies.GreedyQPolicy;
import burlap.behavior.statehashing.DiscreteStateHashFactory;
import burlap.domain.singleagent.gridworld.GridWorldDomain;
import burlap.domain.singleagent.gridworld.GridWorldTerminalFunction;
import burlap.oomdp.singleagent.common.UniformCostRF;
				

public static void main(String [] args){
		
	GridWorldDomain gwd = new GridWorldDomain(3, 3);
	gwd.setMapToFourRooms();
	
	//only go in intended directon 80% of the time
	gwd.setProbSucceedTransitionDynamics(0.8);
	
	Domain domain = gwd.generateDomain();
	
	//get initial state with agent in 0,0
	State s = GridWorldDomain.getOneAgentNoLocationState(domain);
	GridWorldDomain.setAgent(s, 0, 0);
	
	//all transitions return -1
	RewardFunction rf = new UniformCostRF();
	
	//terminate in top right corner
	TerminalFunction tf = new GridWorldTerminalFunction(10, 10);
	
	//setup Q-learning with 0.99 discount factor, discrete state hashing factory, a value
	//function initialization that initializes all Q-values to value 0, a learning rate
	//of 0.1 and an epsilon value of 0.1.
	QLTutorial ql = new QLTutorial(domain, rf, tf, 0.99, new DiscreteStateHashFactory(), 
			new ValueFunctionInitialization.ConstantValueFunctionInitialization(1.), 
			0.1, 0.1);
	
	//run learning for 1000 episodes
	for(int i = 0; i < 1000; i++){
		EpisodeAnalysis ea = ql.runLearningEpisodeFrom(s);
		System.out.println("Episode " + i + " took " + ea.numTimeSteps() + " steps.");
	}
	
	//get the greedy policy from it
	Policy p = new GreedyQPolicy(ql);
	
	//evaluate the policy with one roll out and print out the action sequence
	EpisodeAnalysis ea = p.evaluateBehavior(s, rf, tf);
	System.out.println(ea.getActionSequenceString("\n"));
	
}